Answer:
$2191.12
Explanation:
We are asked to find the value of a bond after 10 years, if you invest $1000 in a savings bond that pays 4% interest, compounded semi-annually.
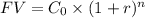 , where,
, where,
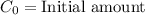 ,
,
r = Rate of return in decimal form.
n = Number of periods.
Since interest is compounded semi-annually, so 'n' will be 2 times 10 that is 20.
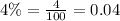

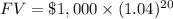
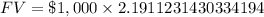
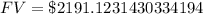

Therefore, the bond would be $2191.12 worth in 10 years.