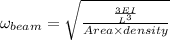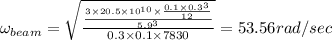Question

Compute the fundamental natural frequency of the transverse vibration of a uniform beam of rectanqular cross section, with one end of the beam is free and one end is fixed. The cross section has a base of 100 mm and height of 300 mm, length of the beam is 5.9 m, E=20.5x10^10 N/m2 and density of 7830 kg/m3. Write your answer in rad/sec with 2 decimal points.

Answer 1

its a lil confusing

Step-by-step explanation:

Answer 2

The natural angular frequency of the rod is 53.56 rad/sec

Step-by-step explanation:

Since the beam is free at one end and fixed at the other hence the beam is a cantilevered beam as shown in the attached figure

We know that when a unit force is placed at the end of a cantilever the displacement of the free end is given by

`\Delta x=(PL^3)/(3EI)`

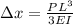
Hence we can write

`P=(3EI\cdot \Delta x)/(L^3)`

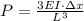
Comparing with the standard spring equation
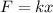`F=kx` we find the cantilever analogous to spring with
`k=(3EI)/(L^3)`

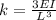
Now the angular frequency of a spring is given by

`\omega =\sqrt{(k)/(m)}`

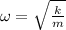
where

'm' is the mass of the load

Thus applying values we get

`\omega _(beam)=\sqrt{((3EI)/(L^(3)))/(Area* density)}`

`\omega _(beam)=\sqrt{((3* 20.5* 10^(10)* (0.1* 0.3^3)/(12))/(5.9^(3)))/(0.3* 0.1 * 7830)}=53.56rad/sec`