Answer:
We can place everything with v(x) on one side of the equality, everything with x on the other side. This is done on the step-by-step explanation, and shows that the new equation is separable.
Explanation:
We have the following differential equation:

We are going to apply the following substitution:
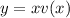
The derivative of y is the derivative of a product of two functions, so
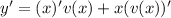
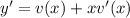
Replacing in the differential equation, we have

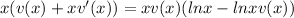
Simplifying by x:
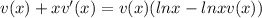
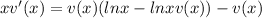

Here, we have to apply the following ln property:
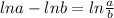
So
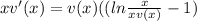
Simplifying by x,we have:
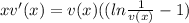
Now, we can apply the above ln property in the other way:
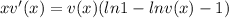
But

So:
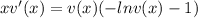
We can place everything that has v on one side of the equality, everything that has x on the other side, so:
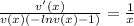
This means that the equation is separable.