Question

The differential equation xy' = y(in x – Iny) is neither separable, nor linear. By making the substitution y(x) = xv(x), show that the new equation for v(x) equation is separable. N.B. you do not have to actually solve the ODE.

Answer 1

We can place everything with v(x) on one side of the equality, everything with x on the other side. This is done on the step-by-step explanation, and shows that the new equation is separable.

Explanation:

We have the following differential equation:

`xy' = y(ln x - ln y)`

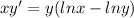
We are going to apply the following substitution:

`y = xv(x)`

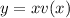
The derivative of y is the derivative of a product of two functions, so

`y' = (x)'v(x) + x(v(x))'`

`y' = v(x) + xv'(x)`

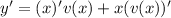
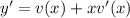
Replacing in the differential equation, we have

`xy' = y(ln x - ln y)`

`x(v(x) + xv'(x)) = xv(x)(ln x - ln xv(x))`

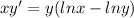
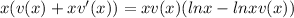
Simplifying by x:

`v(x) + xv'(x) = v(x)(ln x - ln xv(x))`

`xv'(x) = v(x)(ln x - ln xv(x)) - v(x)`

`xv'(x) = v(x)((ln x - ln xv(x) - 1)`

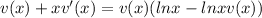
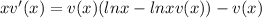
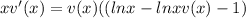
Here, we have to apply the following ln property:

`ln a - ln b = ln (a)/(b)`

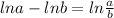
So

`xv'(x) = v(x)((ln (x)/(xv(x)) - 1)`

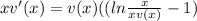
Simplifying by x,we have:

`xv'(x) = v(x)((ln (1)/(v(x)) - 1)`

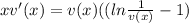
Now, we can apply the above ln property in the other way:

`xv'(x) = v(x)(ln 1 - ln v(x) -1)`

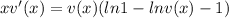
But
`ln 1 = 0`

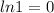
So:

`xv'(x) = v(x)(- ln v(x) -1)`

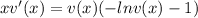
We can place everything that has v on one side of the equality, everything that has x on the other side, so:

`(v'(x))/(v(x)(- ln v(x) -1)) = (1)/(x)`

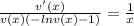
This means that the equation is separable.