Answer:
The flow is turbulent at both the parts of the tube.
Step-by-step explanation:
Given:
Water is flowing in circular tube.
Inlet diameter is
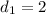 m.
m.
Outlet diameter is
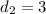 m.
m.
Inlet velocity is
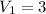 m/s.
m/s.
Kinematic viscosity is
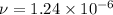 m²/s.
m²/s.
Concept:
Apply continuity equation to find the velocity at outlet.
Apply Reynolds number equation for flow condition.
Step1
Apply continuity equation for outlet velocity as follows:
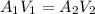
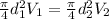
Substitute the values in the above equation as follows:
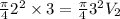
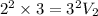
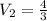 m/s.
m/s.
Step2
Apply Reynolds number formula for the flow condition at inlet as follows:
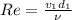

Re=4838709.677
Apply Reynolds number formula for the flow condition at outlet as follows:
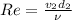
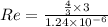
Re=3225806.452
Thus, the Reynolds number is greater than 2000. Hence the flow is turbulent.
Hence, the flow is turbulent at both the parts of the tube.