Answer:
The total distance traveled is 736 m
Solution:
According to the question:
Initial velocity, v = 0
(since, the car is starting from rest)
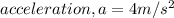
Time taken, t = 8 s
Now, the distance covered by it in 8 s is given by the second eqn of motion:

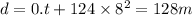
Now, to calculate the velocity, we use eqn 1 of motion:
v' = v + at
v' = 0 + 4(8) = 32 m/s
Now, the distance traveled by the car with uniform velocity of 32 m/s for t' = 19 s:
distance, d' = v't'
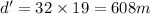
Total distance traveled = d + d' = 128 + 608 = 736 m