Answer:
1) There were 33 $4,000 investors and 27 $8,000 investors.
2) The solution in x = 4, y = 9.
3) There were 24 nickels and 56 dimes.
Explanation:
1) A lawyer has found 60 investors for a limited partnership to purchase an inner-city apartment building, with each contributing either $4,000 or $8,000. If the partnership raised $348,000, then how many investors contributed $4,000 and how many contributed $8,000?
I am going to say that:
x is the number of investors that contributed 4,000.
y is the number of investors that contributed 8,000.
Building the system:
There are 60 investors. So:
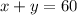
In all, the partnership raised $348,000. So:
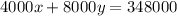
I am going to simplify by 4000. So:
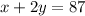
Solving the system:
The elimination method is a method in which we can transform the system such that one variable can be canceled by addition. So:
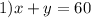
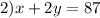
I am going to multiply 1) by -1. So we have
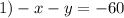
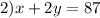
By addition, the x are going to cancel each other
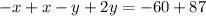

For x:
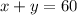
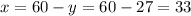
There were 33 $4,000 investors and 27 $8,000 investors.
2) Solve the system by row-reducing the corresponding augmented matrix.
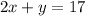
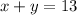
This system has the following augmented matrix:
![\left[\begin{array}{ccc}2&1&17\\1&1&13\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/5uefrje97cicrvzw8q8qumnr3ss05wxs3v.png)
To help the row reducing, i am going to swap the first with the second line:
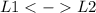
So we have:
![\left[\begin{array}{ccc}1&1&13\\2&1&17\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/2ju4dowgwu91b3b4hd772yqv7fw32xn97m.png)
Now, reducing the first column.
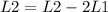
So we have:
![\left[\begin{array}{ccc}1&1&13\\0&-1&-9\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/7fhvbu3e4wmhbql6ihnfk3u4xepp9tlvb6.png)
Now we do:
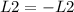
And the matrix is:
![\left[\begin{array}{ccc}1&1&13\\0&1&9\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/vcq8letnaaxq19l70nivtqmbsx3cuevjz4.png)
Now to reduce the second column, we do:
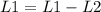
![\left[\begin{array}{ccc}1&0&4\\0&1&9\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/2yxojxecc9tif5zp2pxw56m7p57ln4hydi.png) .
.
So the solution is:
x = 4, y = 9.
3) A jar contains 80 nickels and dimes worth $6.80. How many of each kind of coin are in the jar?
I am going to say that x is the number of nickels and y is the number of dimes.
Each nickel is worth 5 cents and each dime is worth 10 cents.
Building the system:
There are 80 coins in all:
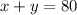
They are worth $6.80. So:
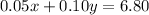
Solving the system:
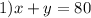
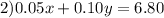
I am going to divide 1) by -10, so we can cancel y. So:
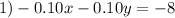
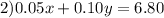
Adding:
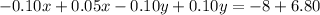
 *(-100)
*(-100)

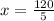
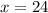
Also
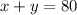

There were 24 nickels and 56 dimes.