Question

Two narrow slits are separated by a distance of 0.10 mm. When illuminated with 550 nm light, a diffraction pattern is observed on a screen 2.2 m from the slits. What is the lateral separation of the first and second order maxima seen on the screen (in cm)?

Answer 1

1.21 cm.

Step-by-step explanation:

Given that the wavelength of light is 550 nm.

And the distance between the slits is 0.10 mm.

And the distance to the screen is 2.2 m.

As we know that the lateral separation can be defined by the formula.

`LS=(m\lambda D)/(d)`

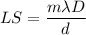
Here, m is the order of maxima,
`\lambda` is the wavelength , d is the distance between the slits and D is the distance to the screen.

For first maxima m=1, and for second maxima m=2.

Difference in the lateral maxima will be,

`\Delta LS=(2\lambda D)/(d)-(1\lambda D)/(d)\\\Delta LS=(\lambda D)/(d)`

Substitute all the variables in the above equation.

`\Delta LS=(550 nm* 2.2m)/(0.10mm)\\\Delta LS=(550* 10^(-9) nm* 2.2m)/(0.10* 10^(-3) )\\ \Delta LS=121* 10^(-4)m\\ \Delta LS=1.21 cm`

Therefore, the lateral separation difference between between first order and second order maxima is 1.21 cm.