Answer: 78.89%
Step-by-step explanation:
Given : Sample size : n= 1200
Sample mean :
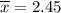
Standard deviation :
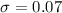
We assume that it follows Gaussian distribution (Normal distribution).
Let x be a random variable that represents the shaft diameter.
Using formula,
 , the z-value corresponds to 2.39 will be :-
, the z-value corresponds to 2.39 will be :-
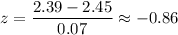
z-value corresponds to 2.60 will be :-
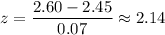
Using the standard normal table for z, we have
P-value =
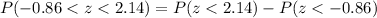
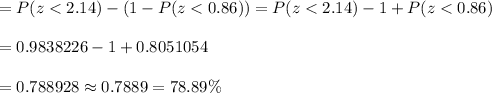
Hence, the percentage of the diameter of the total shipment of shafts will fall between 2.39 inch and 2.60 inch = 78.89%