Question

An engineer measures a sample of 1200 shafts out of a certain shipment. He finds the shafts have an average diameter of 2.45 inch and a standard deviation of 0.07 inch. Assume that the shaft diameter follows a Gaussian distribution. What percentage of the diameter of the total shipment of shafts will fall between 2.39inch and 2.60 inch?

Answer 1

Answer: 78.89%

Step-by-step explanation:

Given : Sample size : n= 1200

Sample mean :
`\overline{x}=2.45`

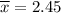
Standard deviation :
`\sigma=0.07`

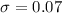
We assume that it follows Gaussian distribution (Normal distribution).

Let x be a random variable that represents the shaft diameter.

Using formula,
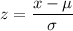`z=(x-\mu)/(\sigma)`, the z-value corresponds to 2.39 will be :-

`z=(2.39-2.45)/(0.07)\approx-0.86`

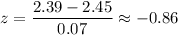
z-value corresponds to 2.60 will be :-

`z=(2.60-2.45)/(0.07)\approx2.14`

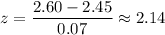
Using the standard normal table for z, we have

P-value =
`P(-0.86<z<2.14)=P(z<2.14)-P(z<-0.86)`

`=P(z<2.14)-(1-P(z<0.86))=P(z<2.14)-1+P(z<0.86)\\\\=0.9838226-1+0.8051054\\\\=0.788928\approx0.7889=78.89\%`

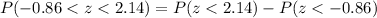
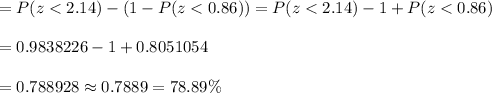
Hence, the percentage of the diameter of the total shipment of shafts will fall between 2.39 inch and 2.60 inch = 78.89%