Question

Find the average rate of change of the function below from x1 to x2.

f(x)=2x+7

from

x1=−1

to

x2=0

Question 9 options:

a)

2

b)

−12

c)

13

d)

-8

e)

none

Answer 1

wala akong alam jun

Explanation:

i hate math, mathuloggggggg ka, ayieee ?luh asa ka

Answer 2

The average rate of change is 2, letter a)

Explanation:

Given a function y, the average rate of change S of y=f(x) in an interval
`[x_(s), x_(f)]` will be given by the following equation:

`S = (f(x_(f)) - f(x_s))/(x_(f) - x_(s))`.

In our problem, we have that:

`f(x) = 2x + 7`

`x_(s) = -1`

`x_(f) = 0`

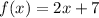
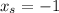
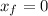
So:

`f(x_(s)) = f(-1) = 2(-1) + 7 = -2 + 7 = 5`

`f(x_(f)) = f(0) = 2(0) + 7 = 0 + 7 = 7`

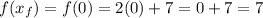
The average rate of change is:

`S = (f(x_(f)) - f(x_s))/(x_(f) - x_(s)) = (7-5)/(0 -(-1)) = (2)/(1) = 1`

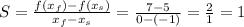
The average rate of change is 2, letter a)