Answer:
The average rate of change is 2, letter a)
Explanation:
Given a function y, the average rate of change S of y=f(x) in an interval
![[x_(s), x_(f)]](https://img.qammunity.org/2020/formulas/mathematics/college/7jqds3ux3mcjnqg0nqvx4gus8aaoib3fw3.png) will be given by the following equation:
will be given by the following equation:
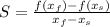 .
.
In our problem, we have that:
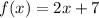
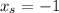
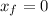
So:
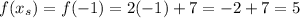
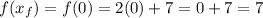
The average rate of change is:
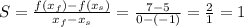
The average rate of change is 2, letter a)