Question

In a combustion furnace, 2094 standard ft3 per hour

of natural gas (Methane) is burned with 6% excess air.
How many standard ft3 of air are drawn from outside
per hour by the fan that supplies the air?

Answer 1

Step-by-step explanation:

The chemical reaction is as follows.

`CH_(4) + 2O_(2) \rightarrow CO_(2) + 2H_(2)O`

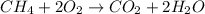
It is given that 2094
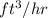`ft^(3)/hr`. And, it is known that 1
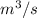`m^(3)/s` = 127133
`ft^(3)/hr`

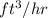
Hence, convert 2094
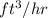`ft^(3)/hr` into
`m^(3)/s` as follows.

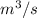`(2094 ft^(3)/hr)/(127133 ft^(3)/hr) * 1 m^(3)/s`

=
`0.0165 m^(3)/s`

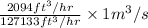
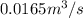
As ideal gas equation is PV = nRT. So, calculate the number of moles as follows.

n =
`(PV)/(RT)`

=
`(1 atm * 0.0165 m^(3))/(0.0821 * 298 K)`

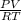
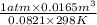
= 0.673 mol/sec

According to the stoichiometry of the given reaction, 1 mol of methane reacts with 2 mol of oxygen.

So, 1 mol
`CH_(4)` = 2 mol
`O_(2)[\tex]</p><p>Hence, [tex]O_(2)[\tex] required theoretically = [tex]2 * 0.673 mol/s` = 1.346 mol/s

Hence, air required theoretically =
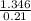`(1.346)/(0.21)` = 6.4095 mol/s.

Since, 6% of excess air is being supplied. Therefore, total air supplied will be calculated as follows.

Total air supplied =
`6.4095 mol/s [1 + (6)/(100)]`

= 6.794 mol/s

Now, calculate the volume using ideal gas law equation as follows.

PV = nRT

`1 atm * V = 6.794 mol/s * 8.21 * 10^(-5) Latm/K mol \6 times 298 K`

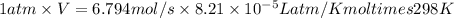
V = 0.166229
`m^(3)/s`

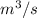
Converting calculated volume into
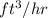`ft^(3)/hr` as follows.

1
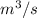`m^(3)/s` = 127133
`ft^(3)/hr`

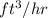
So, 0.166229
`m^(3)/s` =
`0.166229 m^(3)/s * 127133 (ft^(3)/hr)/(1 m^(3)/s)`

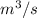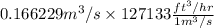
= 21133.191
`ft^(3)/hr`

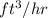
Thus, we can conclude that 21133.191
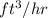`ft^(3)/hr` of air are drawn from outside per hour by the fan that supplies the air.