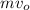Question

The force acting on a particle of mass m is given by

F=kvx
in which k is a positive constant. The particle passes
throughthe origin with speed Vo at time t=0. Find x as a function
oft.

Answer 1

Answer with Explanation:

From newton's second law the acceleration produced by a force on a mass 'm' is given by

`Acceleration=(Force)/(Mass)`

Applying the given values in the above equation we get

`Acceleration=(kvx)/(m)`

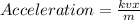
Also we know that acceelration of a particle can ve mathem,atically written as

`a=(v\cdot dv)/(dx)`

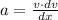
Applying the given values in the above equation we get

`(kvx)/(m)=(v\cdot dv)/(dx)\\\\\Rightarrow {kx}\cdot dx=m\cdot dv\\\\\int kxdx=\int mdv\\\\(kx^2)/(2)=mv-c`

'c' is the constant of integration

whose value is found that at x =0 v=
`v_o`

Thus

`c={mv_o}`

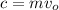
Thus the velocity as a function of position is

`v=(1)/(m)((kx^2)/(2)+c)`

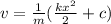
Now by definition of velocity we have

`v=(dx)/(dt)`

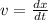
Using the function of velocity in the above relation we get

`(dx)/(kx^(2)+√(2c))=(dt)/(2m)\\\\\int (dx)/((√(k))^2x^(2)+(√(2c))^2)=\int (dt)/(2m)\\\\(1)/(√(2kc))\cdot tan^(-1)(((√(k))x)/(√(2c)))=(t)/(2m)+\phi \\\\`

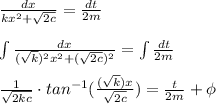
where

`\phi` is constant of integration

Now it is given that at t = 0 ,x = 0

thus from the above equation of position and time we get
`\phi =0`

Thus the position as a function of time is

`x(t)=\sqrt{(2c)/(k)}\cdot tan((kct)/(√(2)m))`

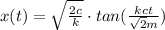
where c=
`mv_o`