Question

Can anyone answer this question

entirely,i.e. work it out and explain it?
A flywheel has a radius of 600 mm, a mass of 144 kg,and a
radius of gyration of 450 mm.. An 18 kg block A is attachedto a
wire that is wrapped around the flywheel, and the system isreleased
from rest. Neglecting the effect of friction,determine (a) the
acceleration of block A, (b) the speed ofblock A after it has moved
1.8 m.

Answer 1

a) 2.18 m/s^2

b) 9.83 m/s

Step-by-step explanation:

The flywheel has a moment of inertia

J = m * k^2

Where

J: moment of inertia

k: radius of gyration

In this case:

J = 144 * 0.45^2 = 29.2 kg*m^2

The block is attached through a wire that is wrapped around the wheel. The weight of the block causes a torque.

T = p * r

r is the radius of the wheel.

T = m1 * g * r

T = 18 * 9.81 * 0.6 = 106 N*m

The torque will cause an acceleration on the flywheel:

T = J * γ

γ = T/J

γ = 106/29.2 = 3.63 rad/s^2

SInce the block is attached to the wheel the acceleration of the block is the same as the tangential acceleration at the eddge of the wheel:

at = γ * r

at = 3.63 * 0.6 = 2.81 m/s^2

Now that we know the acceleration of the block we can forget about the flywheel.

The equation for uniformly accelerated movement is:

X(t) = X0 + V0*t + 1/2*a*t^2

We can set a frame of reference that has X0 = 0, V0 = 0 and the X axis points in the direction the block will move. Then:

X(t) = 1/2*a*t^2

Rearranging

t^2 = 2*X(t)/a

`t = \sqrt{(2*X(t))/(a)}`

`t = \sqrt{(2*18)/(2.81)} = 3.6 s`

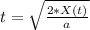
It will reach the 1.8 m in 3.6 s.

Now we use the equation for speed under constant acceleration:

V(t) = V0 + a*t

V(3.6) = 2.81 * 3.6 = 9.83 m/s