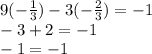Answer:
The solution to this set of linear equations is:
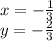
Step-by-step explanation:
This is a system of two equations with two unknown variables x and y, let's call them
Equation 1:
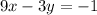
Equation 2:
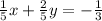
The first step is to solve Equation 1 for y, this means to leave the y alone on one side of the equal
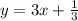
Then with this equation, you can find the value of x by replacing y in Equation 2
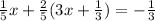
Then simplify this equation to find x
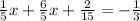
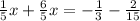
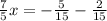
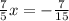
Now you solve for x
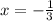
Now you use this value of x to find y
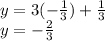
You can check if this answer is correct by replacing the values of x and y into Equation 1 or 2, in this case, let's take Equation 1: