Answer:
The pump operates satisfactorily.
Step-by-step explanation:
According to the NPSH available definition:
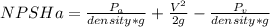
Where:
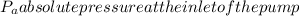
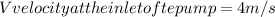
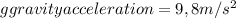

The absolute pressure is the barometric pressure Pb minus the losses: Suction Lift PLift and pipe friction loss Ploss:
To convert the losses in head to pressure:
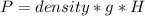
So:
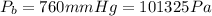
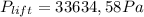

The absolute pressure:
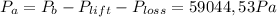
replacing on the NPSH available equiation:
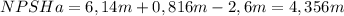
As the NPSH availiable is higher than de required the pump should operate satisfactorily.