Paintball guns were originally developed to mark trees for logging. A forester aims his gun directly at a knothole in a tree that is 4.0 m above the gun. The base of the tree is…

Question

asked Jul 4, 2020 129k views

1 Answer

Kris Markel · Answer 1 · 2020-07-11T04:19:43+0000

Answer:

The distance between knothole and the paint ball is 0.483 m.

Step-by-step explanation:

Given that,

Height = 4.0 m

Distance = 15 m

Speed = 50 m/s

The angle at which the forester aims his gun are,

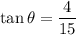
$\tan\theta=(4)/(15)$

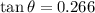
$\tan\theta=0.266$

$\cos\theta=(15)/(√(15^2+4^2))$

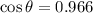
$\cos\theta=0.966$

Using the equation of motion of the trajectory

The horizontal displacement of the paint ball is

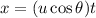
$x=(u\cos\theta)t$

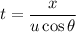
$t=(x)/(u\cos\theta)$

Using the equation of motion of the trajectory

The vertical displacement of the paint ball is

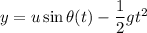
$y=u\sin\theta(t)-(1)/(2)gt^2$

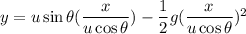
$y=u\sin\theta((x)/(u\cos\theta))-(1)/(2)g((x)/(u\cos\theta))^2$

$y=x\tan\theta-(gx^3)/(2u^2(\cos\theta)^2)$

Put the value into the formula

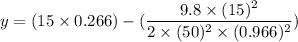
y=(15*0.266)-((9.8*(15)^2)/(2*(50)^2*(0.966)^2))

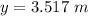
$y=3.517\ m$

We need to calculate the distance between knothole and the paint ball

d=h-y

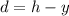
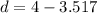
d=4-3.517

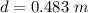
$d=0.483\ m$

Hence, The distance between knothole and the paint ball is 0.483 m.