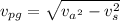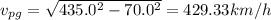Answer:
Speed of the plane over the ground is 429.33 km/hr due West and 70 km/hr towards North
Solution:
According to the question:
Wind flowing in South direction,
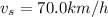
Air speed,
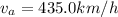
Now,
The velocity vector is required 70 km/h towards north in order to cancel the wind speed towards south.
Therefore,
The ground speed of the plane is given w.r.t fig 1: