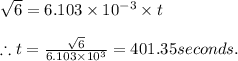Question

Calculate the time taken to completely empty aswimming pool 15

m long and 9 m wide through an opening at thebottom as shown in the
fig. The swimming pool holds water to depth1.5 m.Opening area is
0.3 sq.m and Cd=0.62.

Answer 1

Time needed to empty the pool is 401.35 seconds.

Step-by-step explanation:

The exit velocity of the water from the orifice is obtained from the Torricelli's law as

`V_(exit)=√(2gh)`

where

'h' is the head under which the flow of water occurs

Thus the theoretical discharge through the orifice equals

`Q_(th)=A_(orifice)* √(2gh)`

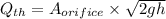
Now we know that

`C_(d)=(Q_(act))/(Q_(th))`

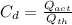
Thus using this relation we obtain

`Q_(act)=C_(d)* A_(orifice)* √(2gh)`

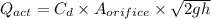
Now we know by definition of discharge

`Q_(act)=(d)/(dt)(volume)=(d(lbh))/(dt)=Lb\cdot (dh)/(dt)`

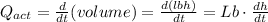
Using the above relations we obtain

`Lb* (dh)/(dt)=AC_(d)* √(2gh)\\\\(dh)/(√(h))=(AC_(d))/(Lb)* √(2g)dt\\\\\int_(1.5)^(0)(dh)/(√(h))=\int_(0)^(t)(0.62* 0.3)/(15* 9)* √(2* 9.81)\cdot dt\\\\`

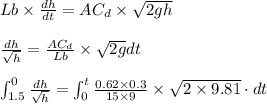
The limits are put that at time t = 0 height in pool = 1.5 m and at time 't' the height in pool = 0

Solving for 't' we get

`√(6)=6.103* 10^(-3)* t\\\\\therefore t=(√(6))/(6.103* 10^(3))=401.35seconds.`