Question

suppose you deposit $1000 in an account paying 4.6% annual interest compounded continuously. How long will it take for the money to double?

Answer 1

Answer: About 16 years

Explanation:

The formula to find the compound amount if compounded continuously is given by :-

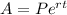`A=Pe^(rt)`, where P is Principal amount, r is the rate of interest ( in decimal) and t is time ( in years).

Given : P= $1000 ; r= 4.6%=0.046

let t be the time it will take to double the amount, the we have

`2(1000)=(1000)e^(0.046* t)`

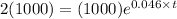
Dividing 1000 both sides, we get

`2=e^(0.046 t)`

Taking natural log on each side, we get

`\ln2=\ln(0.046* t)\\\\\Rightarrow\ 0.6931=0.046t\\\\\Rightarrow\ t=(0.6931)/(0.046)=15.0673913043\approx16\text{ years}`

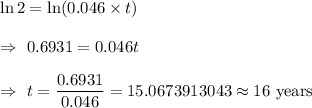
Hence, it will take about 16 years to double the amount.