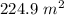Answer:
Explanation:
An isosceles right triangle is a right triangle having two legs (other than hypotenuse ) of same length .
Given : The length of the hypotenuse of an isosceles right triangle is 30 meters.
Let x be the side length of the other two legs, then by using the Pythagoras theorem for right triangle , we have
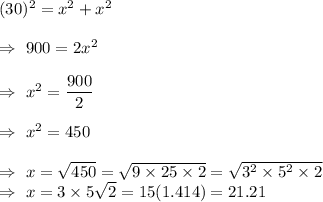
Thus, the other two legs have side length of 21.21 m each.
Now, the area of a right triangle is given by :-
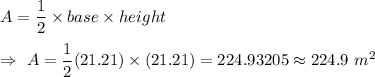
Hence, the area of the given isosceles right triangle=