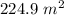Question

The length of the hypotenuse of an isosceles right triangle

is30 meters. Find the area of the triangle. Round to thenearest
tenth, if necessary.

Answer 1

Answer:
`224.9\ m^2`

Explanation:

An isosceles right triangle is a right triangle having two legs (other than hypotenuse ) of same length .

Given : The length of the hypotenuse of an isosceles right triangle is 30 meters.

Let x be the side length of the other two legs, then by using the Pythagoras theorem for right triangle , we have

`(30)^2=x^2+x^2\\\\\Rightarrow\ 900=2x^2\\\\\Rightarrow\ x^2=(900)/(2)\\\\\Rightarrow\ x^2=450\\\\\Rightarrow\ x=√(450)=√(9*25*2)=√(3^2*5^2*2)\\\Rightarrow\ x=3*5√(2)=15(1.414)=21.21`

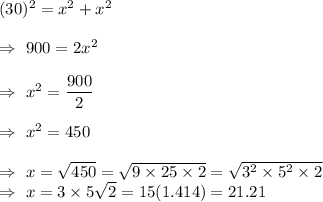
Thus, the other two legs have side length of 21.21 m each.

Now, the area of a right triangle is given by :-

`A=(1)/(2)* base* height\\\\\Rightarrow\ A=(1)/(2)(21.21)*(21.21)=224.93205\approx224.9\ m^2`

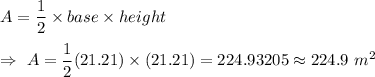
Hence, the area of the given isosceles right triangle=
`224.9\ m^2`