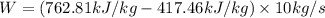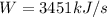Question

Water (10 kg/s) at 1 bar pressure and 50 C is pumped isothermally to 10 bar. What is the pump work? (Use the steam tables.) -7.3 kJ/s O 7.3 kJ/s -210 kJ/s e345 kJ/s 3451 kJ/s

Answer 1

The pump work is 3451 kJ/s

Step-by-step explanation:

Pump work (W) is calculated as

`W = (h_f - h_i) * \dot{m}`

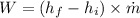
where

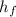`h_f` is the enthalpy of water at its final state

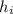`h_i` is the enthalpy of water at its initial state

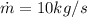`\dot{m} = 10 kg/s` is water mass flow

For liquids, properties are evaluated as saturated liquid. From the figure attached, it can be seen that

`h_f = 762.81 kJ/kg`

`h_i = 417.46 kJ/kg`

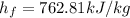
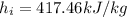
Replacing

`W = (762.81 kJ/kg - 417.46 kJ/kg) * 10 kg/s`

`W = 3451 kJ/s`