Question

The time factor for a doubly drained clay layer

undergoingconsolidation is 0.2
a. What is the degree of consolidation (Uz) at z/H=0.25,
0.5,and 0.75
b. If the final consolidation settlement is expected to be
1.0m, how much settlement has occurred when the time factor is 0.2
andwhen it is 0.7?

Answer 1

Answer with Explanation:

Assuming that the degree of consolidation is less than 60% the relation between time factor and the degree of consolidation is

`T_v=(\pi )/(4)((U)/(100))^2`

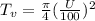
Solving for 'U' we get

`(\pi )/(4)((U)/(100))^2=0.2\\\\((U)/(100))^2=(4* 0.2)/(\pi )\\\\\therefore U=100* \sqrt{(4* 0.2)/(\pi )}=50.46%`

Since our assumption is correct thus we conclude that degree of consolidation is 50.46%

The consolidation at different level's is obtained from the attached graph corresponding to Tv = 0.2

i)
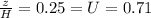`(z)/(H)=0.25=U=0.71` = 71% consolidation

ii)
`(z)/(H)=0.5=U=0.45` = 45% consolidation

iii)
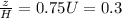`(z)/(H)=0.75U=0.3` = 30% consolidation

Part b)

The degree of consolidation is given by

`(\Delta H)/(H_f)=U\\\\(\Delta H)/(1.0)=0.5046\\\\\therefore \Delta H=50.46cm`

Thus a settlement of 50.46 centimeters has occurred

For time factor 0.7, U is given by

`T_v=1.781-0.933log(100-U)\\\\0.7=1.781-0.933log(100-U)\\\\log(100-U)=(1.780-.7)/(0.933)=1.1586\\\\\therefore U=100-10^(1.1586)=85.59`

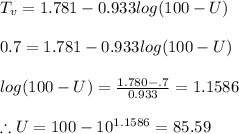
thus consolidation of 85.59 % has occured if time factor is 0.7

The degree of consolidation is given by

`(\Delta H)/(H_f)=U\\\\(\Delta H)/(1.0)=0.8559\\\\\therefore \Delta H=85.59cm`