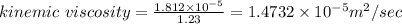Answer:
(a) dynamic viscosity =
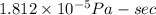
(b) kinematic viscosity =
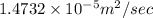
Step-by-step explanation:
We have given temperature T = 288.15 K
Density

According to Sutherland's Formula dynamic viscosity is given by
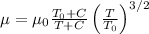 , here
, here
μ = dynamic viscosity in (Pa·s) at input temperature T,
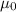 = reference viscosity in(Pa·s) at reference temperature T0,
= reference viscosity in(Pa·s) at reference temperature T0,
T = input temperature in kelvin,
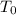 = reference temperature in kelvin,
= reference temperature in kelvin,
C = Sutherland's constant for the gaseous material in question here C =120

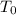 = 291.15
= 291.15
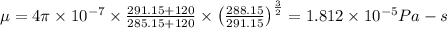 when T = 288.15 K
when T = 288.15 K
For kinematic viscosity :