Question

A particle is moving along a straight line and has an

acceleration of kV^2 m/s^2, where V is the velocity of the
particle. At time t=0, the velocity of the particle = 4m/s, and the
time t=30s the velocity = 26m/s and displacement at time t = Dt
metres. Derive expressions for both velocity and displacement as a
function of time t.

Answer 1

Answer with Explanation:

By definition of acceleration we have

`a=(dv)/(dt)`

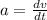
Given
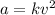`a=kv^(2)`, using this value in the above equation we get

`kv^2=(dv)/(dt)\\\\(dv)/(v^(1))=kdt`

Upon integrating on both sides we get

`\int (dv)/(v^2)=\int kdt\\\\-(1)/(v)=kt+c`

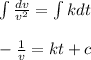
'c' is the constant of integration whose value can be found out by putting value of 't' = 0 and noting V =4 m/s

Thus
`c=-(1)/(4)`

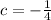
the value of 'k' can be found by using the fact that at t= 30 seconds velocity = 26 m/s

`(-1)/(26)=k* 30-(1)/(4)\\\\\therefore k=((-1)/(26)+(1)/(4))/(30)\\\\k=7.05* 10^(-3)`

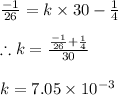
Hence the velocity as a function of time is given by

`v(t)=(-1)/(7.05* 10^(-3)t-(1)/(4))`

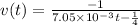
By definition of velocity we have

`v=(dx)/(dt)`

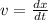
Making use of the obtained velocity function we get

`(dx)/(dt)=(-1)/(kt-(1)/(4))\\\\\int dx=\int (-dt)/(kt-(1)/(4))\\\\x(t)=(-1)/(7.05* 10^(-3))\cdot ln(7.05* 10^(-3)t-(1)/(4))+x_o`

here
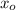`x_o` is the constant of integration