Answer:
Explanation:
First, observe that:
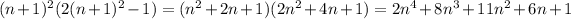
We will prove by mathematical induction that, for every natural,

We will prove our base case (when n=1) to be true.
Base case:

Inductive hypothesis:
Given a natural n,

Now, we will assume the induction hypothesis and then use this assumption, involving n, to prove the statement for n + 1.
Inductive step:
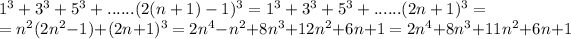
Then, by the observation made at the beginning of this proof, we have that

With this we have proved our statement to be true for n+1.
In conlusion, for every natural n
,

b)
Observe that

Then,
- If

- If
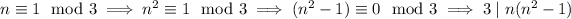
- If
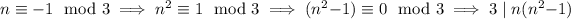
Therefore, for every
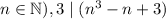
c)
We will prove by mathematical induction that, for every natural n>3,
![(n-1)^2<2n^2.[tex] </p><p>We will prove our base case (when n=4) to be true. </p><p><strong>Base case: </strong></p><p>[tex](n-1)^2=(4-1)^2=9<32=2*4^2=2n^2](https://img.qammunity.org/2020/formulas/mathematics/college/gq3j8ew0fbjpmd6okf975neh487zi7v3wo.png)
Inductive hypothesis:
Given a natural n>4,
[tex](n-1)^2<2n^2.[tex]
Now, we will assume the induction hypothesis and then use this assumption, involving n, to prove the statement for n + 1.
Inductive step:
[tex]((n+1)-1)^2=((n-1)+1)^2=(n-1)^2+2(n-1)+1<2n^2+2(n-1)+1=2n^2+2n- 1<2n^2+2n+1 =2(n+1)^2.[tex]
With this we have proved our statement to be true for n+1.
In conclusion, for every natural n>3,
[tex](n-1)^2<2n^2.[tex]