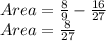Answer:
The area of the region between the curves y=6x^2 and y=4x is 8/27
Explanation:
Use the diagram to visualize the problem, the area colored of blue is the one that needs to be found, let's do it in 3 parts:
Part 1: Find the intersection points of the curves
To do this we put both equations in one and solve it for x:
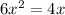
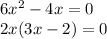
This equation has 2 possible solutions:
x=0 and x=2/3, so the interval for integration is 0 <= x <= 2/3
Part 2: Find the area below each curve
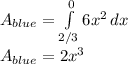 , evaluate in 0 and 2/3
, evaluate in 0 and 2/3
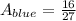
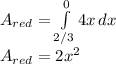 , evaluate in 0 and 2/3
, evaluate in 0 and 2/3
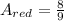
Part 3: Substract the area of the blue curve (y=6x^2) to the area of the red curve (y=4x)