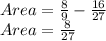Question

What is the area of the region bounded between the curves y=6x^2 and y=4x?

Answer 1

The area of the region between the curves y=6x^2 and y=4x is 8/27

Explanation:

Use the diagram to visualize the problem, the area colored of blue is the one that needs to be found, let's do it in 3 parts:

Part 1: Find the intersection points of the curves

To do this we put both equations in one and solve it for x:

`6x^2=4x`

`6x^2-4x=0\\2x(3x-2)=0`

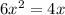
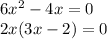
This equation has 2 possible solutions:

x=0 and x=2/3, so the interval for integration is 0 <= x <= 2/3

Part 2: Find the area below each curve

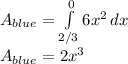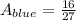
`A_(blue)=\int\limits^0_(2/3) {6x^2} \, dx \\A_(blue)=2x^3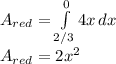`, evaluate in 0 and 2/3

`A_(blue)=(16)/(27)`

`A_(red)=\int\limits^0_(2/3) {4x} \, dx \\A_(red)=2x^2`, evaluate in 0 and 2/3

`A_(red)=(8)/(9)`

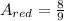
Part 3: Substract the area of the blue curve (y=6x^2) to the area of the red curve (y=4x)

`Area=(8)/(9)-(16)/(27)\\Area=(8)/(27)`