Question

A closed, rigid tank contains 2 kg of water initially at 80 degree C and a quality of 0.6. Heat transfer occurs until the tank contains only saturated vapor at a higher pressure. Kinetic and potential energy effects are negligible. For the water as the system, determine the amount of energy transfer by heat, in kJ.

Answer 1

`Q=1752.3kJ`

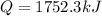
Step-by-step explanation:

Hello,

In this case, the transferred heat is defined via the first law of thermodynamics as shown below as it is about a rigid tank which does not perform any work:

`Q_(in)=m_(H_2O)(u_2-u_1)`

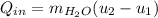
The internal energy at the first state (80°C as a vapor-liquid mixture) is computed based on its quality as follows:

`u_1=334.97kJ/kg+0.6*2146.6kJ/kg=1622.93kJ/kg`

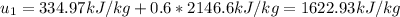
Now, the specific volume turn out into:

`v_1=0.001029m^3/kg+0.6*3.404271m^3/kg=2.0435916m^3/kg`

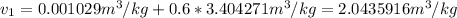
As the volume does not change due to the fact that this is about a rigid tank, we must look for a temperature at which the saturated vapor's volume matches with the previously computed volume. This turn out into a temperature of about 94.17 °C at which the internal energy of the saturated vapor is about (by interpolation):

`u_2=2499.1kJ/kg`

In such a way, the energy transfer by heat is:

`Q=2kg*(2499.1kJ/kg-1622.93kJ/kg)\\Q=1752.3kJ`

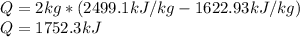
Best regards.