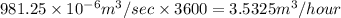Question

A single-cylinder pump feeds a boiler through a delivery

pipeof 25mm internal diameter. the plunger speed is such as togive
a vlocity of 2 m/s. how many m3 ofwater can
be pumped into the boiler in 1 hour?

Answer 1

Net discharge per hour will be 3.5325
`m^3/hr`

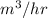
Step-by-step explanation:

We have given internal diameter d = 25 mm

Time = 1 hour = 3600 sec

So radius
`r=(d)/(2)=(25)/(2)=12.5mm=12.5* 10^(-3)m`

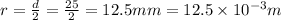
We know that area is given by

`A=\pi r^2=3.14* (12.5* 10^(-3))^2=490.625* 10^(-6)m^2`

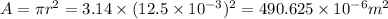
We know that discharge is given by
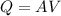`Q=AV`, here A is area and V is velocity

So
`Q=AV=490.625* 10^(-6)* 2=981.25* 10^(-6)m^3/sec`

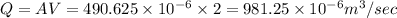
So net discharge in 1 hour =
`981.25* 10^(-6)m^3/sec* 3600=3.5325m^3/hour`