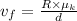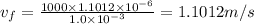Answer:
The velocity of the fluid is 1.1012 m/s
Solution:
As per the question, for the fluid:
Diameter of the capillary tube, d = 1.0 mm =
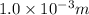
Reynolds No., R = 1000
Kinematic viscosity,
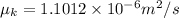
Now, for the fluid velocity, we use the relation:

where
 = velocity of fluid
= velocity of fluid