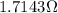Answer:
The total resistance of these three resistors connected in parallel is
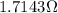
Explanation:
The attached image has the circuit for finding the total resistance. The circuit is composed by a voltage source and three resistors connected in parallel:
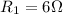 ,
,
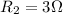 and
and
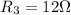 .
.
First step: to find the source current
The current that the source provides is the sum of the current that each resistor consumes. Keep in mind that the voltage is the same for the three resistors (
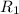 ,
,
 and
and
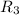 ).
).
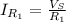
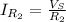
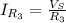
The total current is:

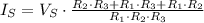
The total resistance (
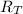 ) is the source voltage divided by the source current:
) is the source voltage divided by the source current:
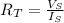
Now, replace
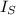 by the previous expression and the total resistance would be:
by the previous expression and the total resistance would be:
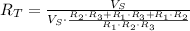
Simplify the expression and you must get:

The last step is to replace the values of the resistors:
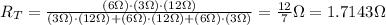
Thus, the total resistance of these three resistors connected in parallel is