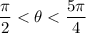Since you want a negative cosine, your angle will surely lie in the II or III quadrant.
In particular, in the II quadrant, the cosine is negative and the sine is positive, so you surely have

As for the third quadrant, we start with
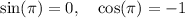
(which implies that the sine is greater than the cosine) and we end with
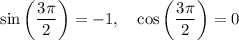
which implies that the sine is less than the cosine.
Halfway through, we have
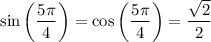
So, only the first half of the III quadrant is fine, because sine and cosine are both negative, but the sine is "less negative" than the cosine, so we have, as requested,
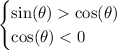
So, the final answer is that the angle lies in the interval