Question

Find the value of a for which the solution of the inequality is all real numbers.

3x+8+2ax≥3ax−4a
How do I solve for a and what does a stand for please help meeeeeee.

Answer 1

`a=3,\text{ then } x\in(-\infty,\infty)\\ \\a\in(-\infty,3),\text{ then }x\in \left[(-4a-8)/(3-a),\infty\right)\\ \\a\in(3,\infty),\text{ then }x\in \left(-\infty, (-4a-8)/(3-a)\right]`

Explanation:

In the inequality

`3x+8+2ax\ge 3ax-4a\ \ \ (1)`

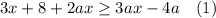
a is an arbitrary real number.

Separate the terms with x into left side and the terms without x in the right side:

`3x+2ax-3ax\ge -4a-8\\ \\3x-ax\ge -4a-8\\ \\(3-a)x\ge -4a-8\ \ \ (2)`

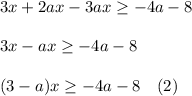
First, look at the leading coefficient at x. If this coefficient is equal to 0 (when
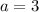`a=3`), then the inequality is

`0\ge -4a-8\\ \\0\ge -12-8\ [\text{Substituted }a=3]\\ \\0\ge -20`

This is true inequality for all x, so at
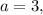`a=3,` the inequality (1) has the solution
`x\in (-\infty,\infty)`

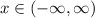
Now, if the leading coefficient

`3-a>0\\ \\a<3,`

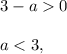
then we can divide the inequality (2) by this positive number
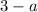`3-a` and get

`x\ge (-4a-8)/(3-a)`

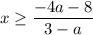
If the leading coefficient

`3-a<0\\ \\a>3,`

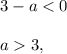
then we can divide the inequality (2) by this negative number
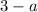`3-a` and get

`x\le (-4a-8)/(3-a)`

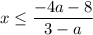
So, the answer is

`a=3,\text{ then } x\in(-\infty,\infty)\\ \\a\in(-\infty,3),\text{ then }x\in \left[(-4a-8)/(3-a),\infty\right)\\ \\a\in(3,\infty),\text{ then }x\in \left(-\infty, (-4a-8)/(3-a)\right]`