Answer:
![a=3,\text{ then } x\in(-\infty,\infty)\\ \\a\in(-\infty,3),\text{ then }x\in \left[(-4a-8)/(3-a),\infty\right)\\ \\a\in(3,\infty),\text{ then }x\in \left(-\infty, (-4a-8)/(3-a)\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/3jad3zthxsr9xouswxu7c6qajvqrnsqnqp.png)
Explanation:
In the inequality
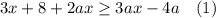
a is an arbitrary real number.
Separate the terms with x into left side and the terms without x in the right side:
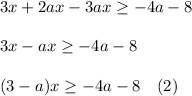
First, look at the leading coefficient at x. If this coefficient is equal to 0 (when
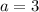 ), then the inequality is
), then the inequality is
![0\ge -4a-8\\ \\0\ge -12-8\ [\text{Substituted }a=3]\\ \\0\ge -20](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ljswhk67pqll08l39or3qfmz2reruk6kue.png)
This is true inequality for all x, so at
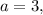 the inequality (1) has the solution
the inequality (1) has the solution
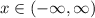
Now, if the leading coefficient
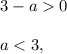
then we can divide the inequality (2) by this positive number
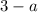 and get
and get
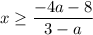
If the leading coefficient

then we can divide the inequality (2) by this negative number
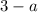 and get
and get
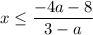
So, the answer is
![a=3,\text{ then } x\in(-\infty,\infty)\\ \\a\in(-\infty,3),\text{ then }x\in \left[(-4a-8)/(3-a),\infty\right)\\ \\a\in(3,\infty),\text{ then }x\in \left(-\infty, (-4a-8)/(3-a)\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/3jad3zthxsr9xouswxu7c6qajvqrnsqnqp.png)