Answer:
The bond's yield to maturity is 9.45% using Excel to get exact values, and 9.59% using approximate method.
Step-by-step explanation:
We can calculate is using 2 ways, using Excel to get the exact percentage or with approximate methods, calculating the semi-annual Yield to Maturity using the following formula
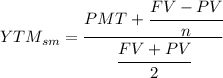
And from there we can calculate the Yield to Maturity just by multiplying the semi-annual one by 2.
Identifying the given information.
We have a period of 30 years, so for the semiannual bond we have
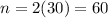 periods.
periods.
The face value, FV, is $1000, the coupon rate is 0.10, thus we can use them to find the interest per period PMT.
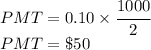
The current price of the bond, PV is $1050.
Replacing the values on the semiannual Yield to Maturity
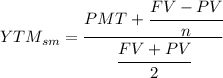
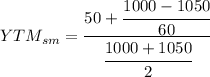
Simplifying we get
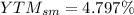
Finding the Yield to Maturity.
We can just multiply by 2 to get the Yield to Maturity from our previous result and rounding it to 2 decimals we get
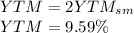
Alternatively we can use Excel and write:
RATE(n, PMT, PV, FV)*2
That is
RATE(60,50,1050,1000)*2
And we will get the exact Yield to maturity 9.49%