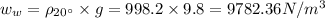Question

The information on a can of pop indicates that the can contains 360 mL. The mass of a full can of pop is 0.369 kg, while an empty can weighs 0.153 N. Determine the specific weight, density, and specific gravity of the pop and compare your results with the corresponding values for water at Express your results in SI units.

Answer 1

Specific weight of the pop,
`w_(s) = 8619.45 N/m^(3)`

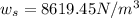
Density of the pop,
`\rho_(p) = 8790.76 kg/m^(3)`

`g_(s) = 8.79076`

`w_(w) = 9782.36 N/m^(3)`

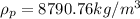
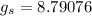
Given:

Volume of pop, V = 360 mL = 0.36 L =
`0.36* 10^(-3) m^(3)`

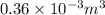
Mass of a can of pop , m = 0.369 kg

Weight of an empty can, W = 0.153 N

Solution:

Now, weight of a full can pop, W

W' = mg =
`0.369* 9.8 = 3.616 N`

Now weight of the pop in can is given by:

w = W' - W = 3.616 - 0.513 = 3.103 N

Now,

The specific weight of the pop,
`w_(s) = (weight of pop)/(volume of pop)`

`w_(s) = (3.103)/(0.36* 10^(- 3)) = 8619.45 N/m^(3)`

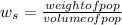
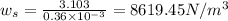
Now, density of the pop:

`\rho_(p) = (w_(s))/(g)`

`\rho_(p) = (86149.45)/(9.8) = 8790.76 kg/m^(3)`

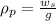
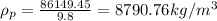
Now,

Specific gravity,
`g_(s) = (\rho_(p))/(density of water, \rho_(w))`

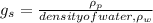
where

`g_(s) = (8790.76)/(1000) = 8.79076`

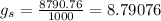
Now, for water at
`20^(\circ)c`:

Specific density of water =
`998.2 kg/m^(3)`

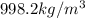
Specific gravity of water =
`0.998 kg/m^(3)`

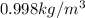
Specific weight of water at
`20^(\circ)c`:

`w_(w) = \rho_(20^(\circ))* g = 998.2* 9.8 = 9782.36 N/m^(3)`