Question

An open vat in a food processing plant contains 500 L of water at 20°C and atmospheric pressure. If the water is heated to 80°C, what will be the percentage change in its volume? If the vat has a diameter of 2 m, how much will the water level rise due to this temperature increase?

Answer 1

percentage change in volume is 2.60%

water level rise is 4.138 mm

Step-by-step explanation:

given data

volume of water V = 500 L

temperature T1 = 20°C

temperature T2 = 80°C

vat diameter = 2 m

to find out

percentage change in volume and how much water level rise

solution

we will apply here bulk modulus equation that is ratio of change in pressure to rate of change of volume to change of pressure

and we know that is also in term of change in density also

so

E =
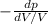`-(dp)/(dV/V)` ................1

And
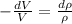`-(dV)/(V) = (d\rho)/(\rho)` ............2

here ρ is density

and we know ρ for 20°C = 998 kg/m³

and ρ for 80°C = 972 kg/m³

so from equation 2 put all value

`-(dV)/(V) = (d\rho)/(\rho)`

`-(dV)/(500*10^(-3) ) = (972-998)/(998)`

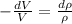
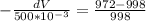
dV = 0.0130 m³

so now % change in volume will be

dV % =
`-(dV)/(V)` × 100

dV % =
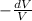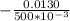`-(0.0130)/(500*10^(-3) )` × 100

dV % = 2.60 %

so percentage change in volume is 2.60%

and

initial volume v1 =
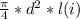`(\pi )/(4) *d^2*l(i)` ................3

final volume v2 =
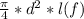`(\pi )/(4) *d^2*l(f)` ................4

now from equation 3 and 4 , subtract v1 by v2

v2 - v1 =
`(\pi )/(4) *d^2*(l(f)-l(i))`

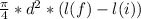
dV =
`(\pi )/(4) *d^2*dl`

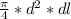
put here all value

0.0130 =
`(\pi )/(4) *2^2*dl`

dl = 0.004138 m

so water level rise is 4.138 mm