Question

For the final days before the election, the campaign manager has a total of $41,500 to spend on TV and radio campaign advertisements. Each TV ad costs $3000 and is seen by 10,000 voters, while each radio ad costs $500 and is heard by 2000 voters. Ignoring repeated exposures to the same voter, how many TV and radio ads will contact 148,000 voters using the allocated funds?

Answer 1

Answer: 9 TV ads and 29 radio ads will contact 148,000 voters using the allocated funds .

Explanation:

Let x denotes the number of users of TV ads and y denotes the number of radio ads.

Then by considering the given information, we have the foolowing system of equation:-

`\text{Number of voters}\ :10000x+2000y=148000----(1)\\\\\text{Total costs}\ :3000x+500y=41500------(2)`

Multiply 4 on both sides of equation (2) , we get

`12000x+2000y=166000---------(3)`

Subtract (1) from (3) , we get

`2000x=18000\\\\\Rightarrow\ x=(18000)/(2000)=9`

Put x= 9 , in (2), we get;

`3000(9)+500y=41500\\\\\Rightarrow\ 27000+500y=41500\\\\\Rightarrow\ 500=14500\\\\\Rightarrow\ y=(14500)/(500)=29`

Hence, the number of TV ads will be 9 and the number of radio ads will will be 29.

Answer 2

Answer: There are 9 T.V. and 29 radio ads.

Explanation:

Since we have given that

Total amount spend on TV and radio = $41,500

Total number of voters using the allocated funds = 148,000

Let the number of TV be 'x'.

Let the number of radio ads be 'y'.

Cost of each TV = $3000

Cost of each radio ads = $500

Number of voters see T.V. = 10,000

Number of voters use radio = 2000

So, According to question, it becomes,

`3000x+500y=\$41500\implies\ 30x+5y=415\\\\10000x+2000y=148000\implies 10x+2y=148`

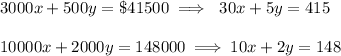
Using the graphing method, we get that

These two lines are intersect at (9,29).

Hence, there are 9 T.V. and 29 radio ads.