Answer:
He would to jog 5 miles to go direct to his home
Explanation:
* Lets explain how to solve the problem
- Charlie jogs 3 miles south and then 4 miles west
- We need to know if Charlie were to jog straight home, without
changing direction how far he have to jog
- Remember: the East-west line is perpendicular to the north-south line
∵ He jogs 3 miles south
∵ He jogs 4 miles west
∵ South ⊥ west
- We can consider that the west and east distance with the straight
distance to home formed a right triangle its legs are the south and
west distance and the straight distance is its hypotenuse
∴ By using Pythagoras Theorem we can find the straight distance
- Remember: In Pythagoras Theorem

where c is the hypotenuse , a and b are the legs of the right Δ
∴ The straight distance =
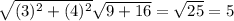
∴ He would to jog 5 miles to go direct to his home