Question

Find the point on the sphere (x+5)^2 + y^2 + (z−9)^2 = 99 nearest to

(a) the​ xy-plane.
(b) the point (−9,0,9).

Answer 1

a) Since the sphere intersects the xy-plane then the set of points of the sphere nearest to the xy-plane is the set of points in the circumference
`(x+5)^2+y^2=18`.

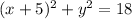b)(-14.9, 0, 9 )

Explanation:

a) The centre of the sphere is (-5,0,-9) and the radio of the sphere is
`√(99) \sim 9.9`. Since |-9|=9 < 9.9, then the sphere intersect the xy-plane and the intersection is a circumference.

Let's find the equation of the circumference.

The equation of the xy-plane is z=0. Replacing this in the equation of the sphere we have:

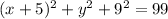`(x+5)^2+y^2+9^2=99`, then
`(x+5)^2+y^2=18`.

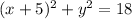b) Observe that the point (-9,0,9) has the same y and z coordinates as the centre and the x coordinate of the point is smaller than that of the x coordinate of the centre. Then the point of the sphere nearest to the given point will be at a distance of one radius from the centre, in the negative x direction.

(-5-
`√(99)`, 0, 9)= (-14.9, 0, 9 )