Answer:
x =(3-√-75)/-6=1/-2+5i/6√ 3 = -0.5000-1.4434i
x =(3+√-75)/-6=1/-2-5i/6√ 3 = -0.5000+1.4434i
Explanation:
Rearrange:
Rearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation :
0-(3*x^2+3*x+7)=0
Step by step solution:
Step 1:
Equation at the end of step 1 :
0 - ((
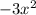+ 3x) + 7) = 0
Step 2:
Pulling out like terms:
2.1 Pull out like factors:
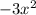- 3x - 7 = -1 • (
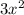+ 3x + 7)
Trying to factor by splitting the middle term
2.2 Factoring
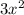+ 3x + 7
The first term is,
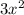its coefficient is 3 .
The middle term is, +3x its coefficient is 3 .
The last term, "the constant", is +7
Step-1 : Multiply the coefficient of the first term by the constant 3 • 7 = 21
Step-2 : Find two factors of 21 whose sum equals the coefficient of the middle term, which is 3 .
-21 + -1 = -22
-7 + -3 = -10
-3 + -7 = -10
-1 + -21 = -22
1 + 21 = 22
3 + 7 = 10
7 + 3 = 10
21 + 1 = 22
Observation : No two such factors can be found !!
Conclusion : Trinomial can not be factored
Equation at the end of step 3 :
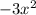- 3x - 7 = 0
Step 3:
Parabola, Finding the Vertex:
3.1 Find the Vertex of y =
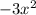-3x-7
For any parabola,Ax2+Bx+C,the x -coordinate of the vertex is given by -B/(2A) . In our case the x coordinate is -0.5000
Plugging into the parabola formula -0.5000 for x we can calculate the y -coordinate :
y = -3.0 * -0.50 * -0.50 - 3.0 * -0.50 - 7.0
or y = -6.250
Parabola, Graphing Vertex and X-Intercepts :
Root plot for : y =
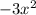-3x-7
Axis of Symmetry (dashed) {x}={-0.50}
Vertex at {x,y} = {-0.50,-6.25}
Function has no real roots
Solve Quadratic Equation by Completing The Square
3.2 Solving
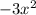-3x-7 = 0 by Completing The Square .
Multiply both sides of the equation by (-1) to obtain positive coefficient for the first term:
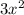+3x+7 = 0 Divide both sides of the equation by 3 to have 1 as the coefficient of the first term :
+x+(7/3) = 0
Subtract 7/3 from both side of the equation :
+x = -7/3
Now the clever bit: Take the coefficient of x , which is 1 , divide by two, giving 1/2 , and finally square it giving 1/4
Add 1/4 to both sides of the equation :
On the right hand side we have :
-7/3 + 1/4 The common denominator of the two fractions is 12 Adding (-28/12)+(3/12) gives -25/12
So adding to both sides we finally get :
+x+(1/4) = -25/12
Adding 1/4 has completed the left hand side into a perfect square :
+x+(1/4) =
(x+(1/2)) • (x+(1/2)) =
(x+(1/2))2
Things which are equal to the same thing are also equal to one another. Since
+x+(1/4) = -25/12 and
+x+(1/4) = (x+(1/2))2
then, according to the law of transitivity,
(x+(1/2))2 = -25/12
We'll refer to this Equation as Eq. #3.2.1
The Square Root Principle says that When two things are equal, their square roots are equal.
Note that the square root of
(x+(1/2))2 is
(x+(1/2))2/2 =
(x+(1/2))1 =
x+(1/2)
Now, applying the Square Root Principle to Eq. #4.2.1 we get:
x+(1/2) = √ -25/12
Subtract 1/2 from both sides to obtain:
x = -1/2 + √ -25/12
√ 3 , rounded to 4 decimal digits, is 1.7321
So now we are looking at:
x = ( 3 ± 5 • 1.732 i ) / -6
Two imaginary solutions :
x =(3+√-75)/-6=1/-2-5i/6√ 3 = -0.5000+1.4434i
or:
x =(3-√-75)/-6=1/-2+5i/6√ 3 = -0.5000-1.4434i