Question

Interstellar space (far from any stars) contains atomic hydrogen (H) with a density of 1 atom/cm3 and at a temperature of about 2.7 K. Determine (a) the pressure in interstellar space, (b) root-mean square speed of the atoms and (c) The kinetic energy stored in 1 km3 of space.

Answer 1

Step-by-step explanation:

Given that,

Number density
`n= 1\ atom/cm^(3) =10^(6)\ atom/m^3`

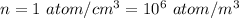
Temperature = 2.7 K

(a). We need to calculate the pressure in interstellar space

Using ideal gas equation

`PV=nRT`

`P=(nRT)/(V)`

`P=(10^(6)*8.314*2.7)/(6.023*10^(23))`

`P=3.727*10^(-17)\ Pa`

`P=36.78*10^(-23)\ atm`

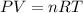
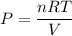
The pressure in interstellar space is
`36.78*10^(-23)\ atm`

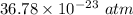
(b). We need to calculate the root-mean square speed of the atom

Using formula of rms

`v_(rms)=\sqrt{(3RT)/(Nm)}`

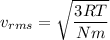
Put the value into the formula

`v_(rms)=\sqrt{(3*8.314*2.7)/(1.007*10^(-3))}`

`v_(rms)=258.6\ m/s`

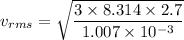
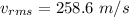
The root-mean square speed of the atom is 258.6 m/s.

(c). We need to calculate the kinetic energy

Average kinetic energy of atom

`E=(3)/(2)kT`

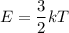
Where, k = Boltzmann constant

Put the value into the formula

`E=(3)/(2)*1.38*10^(-23)*2.7`

`E=5.58*10^(-23)\ J`

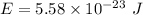
The kinetic energy stored in 1 km³ of space is
`5.58*10^(-23)\ J`.

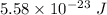Hence, This is the required solution.