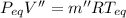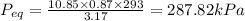Question

A 1-m3 tank containing air @ 25 oC & 500 kPa is connected to another tank containing 5 kg of air at 35 oC & 200 kPa through a valve. The valve is opened and the whole system is brought to thermal equilibrium with the surrounding of 20 oC. Determine the volume of the second tank and the final equilibrium pressure of air. Take air gas constant (R) = 0.287 kJ/(kg.oK)

Answer 1

Volume of Tank 2, V' =
`2.17 m^(3)`

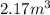
Equilibrium Pressure,
`P_(eq) = 278.82 kPa`

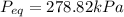
Given:

Volume of Tank 1, V = 1
`m^(3)`

Temperature of Tank 1, T =
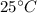`25^(\circ)C` = 298 K

Pressure of Tank 1, P = 500 kPa

Mass of air in Tank 2, m = 5 kg

Temperature of tank 2, T' =
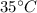`35^(\circ)C` = 303 K

Pressure of Tank 2, P' = 200 kPa

Equilibrium temperature,
`20^(\circ)C` = 293 K

Solution:

For Tank 1, mass of air in tank can be calculated by:

PV = m'RT

`m' = (PV)/(RT)`

`m' = (500* 1)/(0.287* 298) = 5.85 kg`

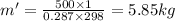
Also, from the eqn:

PV' = mRT

V' = volume of Tank 2

Thus

V' =
`(mRT)/(P)`

V' =
`(5* 0.287* 303)/(200) = 2.17 m^(3)`

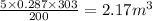
Now,

Total Volume, V'' = V + V' = 1 + 2.17 = 3.17
`m^(3)`

Total air mass, m'' = m + m' = 5 + 5.85 = 10.85 kg

Final equilibrium pressure, P'' is given by:

`P_(eq)V'' = m''RT_(eq)`

`P_(eq) = (m''RT_(eq))/(V'')`

`P_(eq) = (10.85* 0.87* 293)/(3.17) = 287.82 kPa`

`P_(eq) = 287.82 kPa`