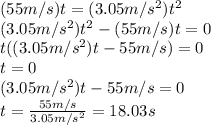Question

After robbing a bank, a criminal tries to escape from the police by driving at a constant speed of 55 m/s (about 125 mph). A police officer, initially at rest, starts chasing the criminal when he drives by, accelerating at a constant rate of 6.1m/s2. How long will it take the officer to catch the criminal?

Answer 1

18.03 s

Step-by-step explanation:

We have two different types of motions, the criminal moves with uniform motion while the police do it with uniformly accelerated motion. Therefore we will use the equations of these cases. We know that by the time the police reach the criminal they will have traveled the same distance.

`x=vt\\x=x_(0)+v_(0)t+(a)/(2)t^2`

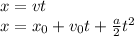
The distance between the police and the criminal when the first one starts the persecution is 0, its initial speed is also zero. So:

`x=(55m/s)t\\x=(6.1m/s^2)/(2)t^2=(3.05m/s^2)t^2`

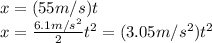
Equalizing these two equations and solving for t:

`(55m/s)t=(3.05m/s^2)t^2\\(3.05m/s^2)t^2-(55m/s)t=0\\t((3.05m/s^2)t-55m/s)=0\\t=0 \\(3.05m/s^2)t-55m/s=0\\t=(55m/s)/(3.05m/s^2)=18.03 s`