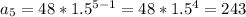Question

What is a formula for the nth term of the given sequence? 48, 72, 108​

Answer 1

`a_n=48*1.5^(n-1)`

Explanation:

Geometric Sequence

In geometric sequences, each term is found by multiplying (or dividing) the previous term by a fixed number, called the common ratio.

We are given the sequence:

48, 72, 108, ...

The common ratio is found by dividing the second term by the first term:

`r=(72)/(48)=1.5`

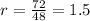
To ensure this is a geometric sequence, we use the ratio just calculated to find the third term a3=72*1.5=108.

Now we are sure this is a geometric sequence, we use the general term formula:

`a_n=a_1*r^(n-1)`

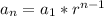
Where a1=48 and r=1.5

`\boxed{a_n=48*1.5^(n-1)}`

For example, to find the 5th term:

`a_5=48*1.5^(5-1)=48*1.5^(4)=243`