Question

At Central Online High School, 4510045100 of the students have a dog, 3010030100 have a cat, and 1810018100 have both a dog and a cat. What is the probability that a student who has a dog also has a cat? Enter your answer as a reduced fraction with the / symbol, like this: 3/14

Answer 1

3/5

Explanation: I just did the test and got it right. This was after I tried 2/5 and got it wrong.

Answer 2

Answer:
`(2)/(5)`

Explanation:

Given : The proportion of students have a dog :
`P(D)=(45)/(100)`

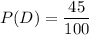
The proportion of students have a cat :
`P(C)=(30)/(100)`

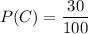
The proportion of students have both a dog and a cat :
`P(C\cap D)=(18)/(100)`

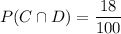
Now, the conditional probability that a student who has a dog also has a cat will be :-

`P(C|D)=(P(C\cap D))/(P(D))\\\\\\\Rightarrow\ P(C|D)=((18)/(100))/((45)/(100))\\\\\\\Rightarrow\ P(C|D)=(18)/(45)=(2)/(5)`

Hence, the probability that a student who has a dog also has a cat =
`(2)/(5)`