Answer:

Explanation:
Given : The proportion of students have a dog :
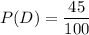
The proportion of students have a cat :
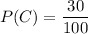
The proportion of students have both a dog and a cat :
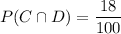
Now, the conditional probability that a student who has a dog also has a cat will be :-
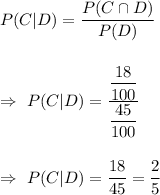
Hence, the probability that a student who has a dog also has a cat =
